Decay of a Substance Model (Blog #4 Decay of a Substance)

      We can not avoid death because life has a limit. We are only living temporarly in God's Wonderland. Decomposition is a process of which a human, animal or any living things decay one's flesh after death. Even in this situation, we can apply a specific function to examine and can model a real life phenomenon. 

      Exponential decay model is used if a quantity is falling rapidly toward zero, without ever reaching zero. We should use the formula,

$\displaystyle y={A}_{0}{e}^{kt}$ where $\displaystyle {A}_{0}$ is the starting value, and e is Euler’s constant. Now k is a negative constant that determines the rate of decay. We may use the exponential decay model when we are calculating half-life, or the time it takes for a substance to exponentially decay to half of its original quantity. We use half-life in applications involving radioactive isotopes. (any of several species of the same chemical element with different masses whose nuclei are unstable and dissipate excess energy by spontaneously emitting radiation in the form of alpha, beta, and gamma rays. ~ http//www.britannica.com/science/radioactive-isotope)

       We used the information gathered through careful observation and measurement in constructing points on a graphs for us to have a function in making a mathematical model.  Exponential decay graphs composes of distinctive shape, as you can see in figure 1. It is essential to not forget that, however each part of the graph lies on the x - axis, it does have a small distance above the x - axis.

Figure 1. A graph showing exponential decay. The equation is $\displaystyle y=3{e}^{-2x}$.

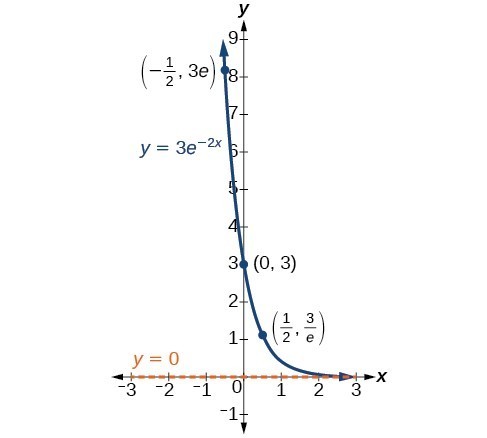
 Exponential Decay. One of the common terms associated with exponential decay, as stated above, is half-life, the length of time it takes an exponentially decaying quantity to decrease to half its original amount. 

To find the half-life of a function describing exponential decay, solve the following equation:

$\displaystyle \frac{1}{2}{A}_{0}={A}_{o}{e}^{kt}$

We find that the half-life depends only on the constant k and not on the starting quantity $\displaystyle {A}_{0}$.

The formula is derived as follows

$\{\begin{array}{cc}\frac{1}{2}{A}_0=A_o{e}^{kt}& \\ \frac{1}{2}=e^{kt}& \text{Divide by}{A}_0.\\ ln\left(\frac{1}{2}\right)=kt& \text{Take the natural log}.\\ -ln\left(2\right)=kt& \text{Apply laws of logarithms}.\\ -\frac{ln\left(2\right)}{k}=t& \text{Divide by}k.\end{array}$

Since t, the time, is positive, k must, as expected, be negative. This gives us the half-life formula

$\displaystyle t=-\frac{\mathrm{ln}\left(2\right)}{k}$

HOW TO: GIVEN THE HALF-LIFE, FIND THE DECAY RATE.